いかん・・・・とうとう夢の中でプログラムを作り始めやがった・・・。
2桁の割り算をするプログラム。
u = 10*s + t
として、
while文で、( u < 10*s )となるまで、sを1ずつ増やしていく。
( u < 10*s )となったら、
u = 10 (s - 1) + t であり、
t = u - 10 (s - 1) となる。
ところがね、n桁の場合はどうすんだと。
for 文でiを0から10まで回して、
中身は、
if (10^(n-1) < u < 10^n)だったら、
check[i] = true
とかにして、
if(check[i] == true) だったら、 n = (check[i]の中身の数字)
として、次のif文で、
u = num[j]*n + num[j]*(n-1)+...+num[j]*1
について、nから始めて一回終わったら n = n-1 と設定して一桁ずつ、減らしていけば、できるはず。
うーん、でも、なんかもうちょっと簡単にできそうな気がするね。
と言う私は、実験屋でありたいなぁ、と思う今日この頃。
 [0回]
[0回]
なかまくらです。
ふと疑問に思ったのですが、
0って、なんで0って書くんですかね。
数字を必要としたのはきっと、そこにものがあったからでしょう。
[りんご]
と
[りんご] [りんご]
を見比べて、
[りんご]
よりも、
[りんご] [りんご]
のほうがたくさんあるね。
[りんご] [りんご]
よりも、
[りんご] [りんご] [りんご]
のほうがたくさんあるね。じゃあ、それぞれ、
[りんご] 1個
[りんご] [りんご] 2個
[りんご] [りんご] [りんご] 3個
としよう、と決めよう、となったんだと思うんです。0が生まれたのは、まだもう少し後の話。
2個の [りんご] の1個を食べました。残りは1個になりました。
1個の [りんご] の1個を食べました。残りは になりました。
「あれっ、どうしたらいいんだ? 1個もないぞ。」
「バカだなぁ、1個ある [りんご] を 1個食べちゃったら、なくなるさ」
「じゃあさ、なくなったのは、どういう風に表したらいいの?」
( [りんご] - [りんご] = ? )
ここで、誰かが考えたわけです。「0」と表そう、と。
でも、きっとアルファベットがあったら、Hになったんじゃないだろうか、と私は妄想します。
なぜって?
「1ー1」 → 「H」 てな、感じにね。
そんな文明を少し夢見た。
 [1回]
[1回]
なかまくらです。
ネタ元(http://nlab.itmedia.co.jp/nl/articles/1205/02/news017.html)
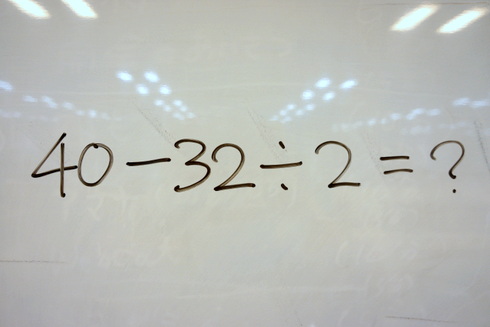
40 - 32 ÷ 2 = ?
...= 4!
そう、4の階乗です。しかしね。
四則演算がよく分かってなくて、
(40-32)/2 = ?
と計算すると、4。
ほほう。
じゃあ、実際にそういう組み合わせの解はいくつあるの? と考えてみる。
つまり、
(m ÷ n) / a = b
且つ
m - n / a = b!
これが、なかなかうまい具合に文字式で表せないので(行列は苦手だ・・・)、プログラムを組んで、100までの総当たりしてみる。
Rubyで組んだプログラムは、一番下に載せてます。(ただし、2の階乗以下は多すぎるので除外)
・・・計算が終わる気配がない(笑)
結果はおって報告する! ・・・かも
ででーん。計算終わり。
さて。結果は・・・
m n a b
25 5 5 4
30 18 3 4
40 32 2 4
でしたー。おもしろー。
if ARGV.length<1
print "Usage: kumiawase.rb <max>\n"
exit
end
max=ARGV[0].to_i
print("0\n")
open("kumiawase.out","w"){|out|
out.print "m n a b","\n"
for m in 1 .. max
print("\n---",m,"\n")
for n in 1 .. max
#print(n," ")
for a in 1 .. max
#print(a,"\n")
bk = 1
for b in 1 .. max
bk = bk*b
#print("\n",bk,"\n")
if b >= 3
if b == (m - n).quo(a)
if bk == m - n.quo(a)
out.print m," ",n," ",a," ",b,"\n"
end
end
end
end
end
end
 [2回]
[2回]
ロケットが宇宙を飛ぶのは、運動量保存の法則によるものです。
ところが、作用反作用の法則でも説明できます。
そりゃあ作用にはかならず反作用があるよ、
となんとなく直感的には分かるのですが、
反作用に当たる力はなんだろう、と考えるとちょっとややこしい。
そこで、簡単な説明は、私は、運動量の保存だと思うのです。
以下に、それを説明します。
ロケットが飛ぶときに、ちょっと不思議なのは、
ロケットって、ジェットを噴射する方と逆向きに進むじゃないですか。

普通の物体は、押されると、押された方に動く。これが普通。
つまり、
ジェットを噴射しているロケットは何かから力を受けないといけないわけです。
ジェットを噴射しているのだから、それがロケットを押してる力なんじゃないの?
と、思われると思いますが、よく考えてください。
ジェット噴射は、ロケットが何かを押している力であって、
ロケットを何かが押す力ではないんですよね。
問題は、分かっていただけましたでしょうか? ややこしいですよね。
まあ、問題は分かったとして、先に進みましょう。
では、何故、ロケットが押す力で、ロケットが飛んでいくのか。
これ、直感的に思い浮かべる現象があるんです。それは、ニュートンの運動の第三法則。
作用反作用の法則。

ローラーブレードに乗った人が、壁を押すと、壁が押し返す力によって、
押しているはずの人間の方が動いてしまう。
力を加えた方向と逆向きに。
もう一度確認しますが、
ロケットは、ジェットを噴射する(押す方向)と逆向きに進むんですよね?
おっ、いいじゃん。これじゃん。ばっちぐーじゃん。というのは、早とちり。
この場合の作用と反作用はなんでしょうか?

作用が、ジェット噴射で、反作用が、、、あれ? 反作用は?
何が、壁の役割をして、ロケットを押し返しているんでしょうか?
空気? でも、宇宙空間でも飛ぶんだぜ?
だったら、むしろ、両方とも 作用?

爆発の力でロケットが作用を受けているというのか?
でも、ロケットって、こんなシンプルな噴射口してないし、
こんな爆発に耐えられるものなのか・・・。
きっとこれじゃあ、宇宙に行く前にバラバラになっちゃうよね!
では、こんなのはどうでしょう?
・・・というわけで、運動量保存の法則の登場です。
式は後に補足しておきます。興味があったら見てみてください。
まあ、運動量保存の法則がどんなものかといいますと、
ボールをもって、台車に乗った人がいます。
簡単のために台車は止まってるとします。

ボールを投げます。

すると、ボールは運動量 p をもって、飛んでいくわけですが、
ボールを投げた人間も、逆向きに同じ大きさの運動量 p をもって、動いてしまうわけです。
これが運動量保存の法則です。
・・・ということはですよ。
ロケットの場合は、噴射するガスが、ボールに対応して、
ロケットが、ボールを投げた人間に対応するわけです。

なんとなーく、運動量保存の法則な気がしてくるでしょう?
つまり、ガスを噴射するとき、運動量は保存されるはずだから、
ロケットは、ガスと逆向きに動かないとおかしいわけです。
なんでおかしいかは、宇宙を作った人に聞いてください。
・・・というのもちょっとアレなので、
もうちょっと考察を深めてみましょう。息はまだ持ちますか?
さて。
もうちょっと直感に訴える説明をすると、勢いよくジェットを噴射するための反動で、
ロケットが逆向きに動いていく・・・・と言うことですよね。
ん? ・・・この説明の仕方って、作用反作用ジャナイカ?
・・・もうちょっと考えてみましょう。
ここでいう運動量保存の法則と、作用反作用の法則は、別物なのか?
作用には逆向きの作用が必ずある、というのは、なんとなくその通りになっているような?
では、台車に乗ってボールを投げる時をもう一度考えてみましょう。

ほら、ボールが受ける力と逆向きで同じ大きさの力を人間が受けて、
台車が動き出すと考えれば、作用反作用の法則に従っているように見えますね。
ということは、結局、作用反作用の法則と運動量保存の法則は同じものなのか?
壁を押す場合を考えましょう。

壁を押すときは、台車だけが動いて、見かけ上運動量は保存されていません。
でも、本当は、壁は少しへこんで振動をはじめます。
つまり、押した瞬間は、運動量は保存されています。
というわけで、作用反作用の法則と運動量保存則はどうやら、同じような性質をもっているようです。(補足参照)
(運動量保存は、第三法則ではなくて、第二法則から導かれるのにね)
というわけで結局、
作用反作用の法則で説明するなら、
ガスを噴き出すための力の反作用で、ロケットが飛んでいる。(補足参照)
トランポリンを逆さまに抱えて跳び箱にかぶせたら、トランポリンのほうが飛んでっちゃうみたいなイメージです(どんなイメージだよ)
運動量保存の法則で説明するなら、
噴き出したガスの運動量と逆向きで同じだけの大きさの運動量をロケットは持つから、それによって、ロケットは飛んでいる。
と、なりますね。言葉で書くと、実は複雑さはあんまり変わらない?笑
式で書くなら、確実に運動量保存の法則の方が素敵ですけどね。
補足
(ちょっと補足:運動量を与えるには、力積が必要。
m v’ ーm v = F t
t=1とすれば、最初速度0だったガスが、t=1で、速度 v になるとき、
F = m v の力をロケットはジェット噴射のガスに加えている。
一方、最初速度0だったガスが、t=1で、速度 v になるとき、
その加速度は a = (v-0)/1=v
よって、運動方程式は、F=m a = m v となるとも証明できる。
つまり、ジェットに p = m v の運動量を与えるために必要な力には、
もちろん逆向きの反作用がある。これが、ロケットが受ける反作用にあたる)
***
運動量保存の法則の式
運動方程式は

これは、こんな風にも書けるわけです。

・・・・・・・・・・・・①
運動量 p は、

変形して、

これを ① に代入して、変形すると、

となるわけです。ここで、 F(外力)=0 としました。
外力というのは、物体の外から、物体に対してくわえられた力のことで、今の場合、F=0です。
 [47回]
[47回]
ねえねえ、皆さん。
私ね、この恥ずかしー間違いを告白しちゃいます。
水の沸点は100℃ですね。融点は0℃
でもね、正確には98℃なんだと思っていたんです。
どこかで聞いた気がするんですよね。
実際に実験してみると、温度計の温度は98℃より上になることはなかったわけです。
で。
たまたま調べる機会があって、調べてみると、沸点はどうも、100℃であってるのでした。
では、なぜ、理科室の実験でそうならないか。
それは、温度計は、赤い液溜まりのところだけをお湯につけているだけでは、正確には測れないということでした。
空気中に出ている部分で冷やされちゃうんですね。
全体をお湯につけた実験をされている方がいらっしゃって、なっとくん。
ははー。
そのサイトは、こちら。下
http://suzukiq.blog.ocn.ne.jp/index/2008/02/100_95bf.html?cid=35764628#comment-35764628
 [2回]
[2回]
