【高校物理】万有引力の法則の導出についての一考
なかまくらです。
万有引力の導出の授業をするときに、毎年しっくりきていなかったのですが、
自分なりに少し理解が進んだように思うので、記録しておこうと思います。
具体的には、万有引力の導出で私が毎年もやっとしていたポイントは、
惑星の向心力を求めた後、作用反作用の法則から、太陽についても同じように力が働くので・・・と論を運ぶところにあります。
しかも、太陽は円運動していないのに、円運動から導出した万有引力の式を
そのまま使ってよいのか(しかも、ちゃっかり、惑星の質量を太陽の質量に置き換えている)
これについて、次のように、考えてみました。
さて。
万有引力の導出は、
(ⅰ)惑星の円運動の運動方程式
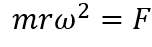
(ⅱ)ケプラーの第三法則
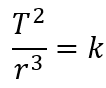
この2つの式を同時に満たす関係式を作ることから、
惑星に働く向心力(万有引力)を求めるという手順で進めていきます。
(ⅱ)式を変形して、
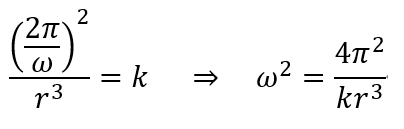
これを(ⅰ)式に代入して、整理すれば、惑星に働く向心力が
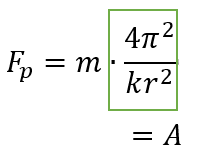
と求まるわけですが、ここで、質量 m 以外の部分は、運動方程式 ma = F であることから、
加速度を表しているはずです。
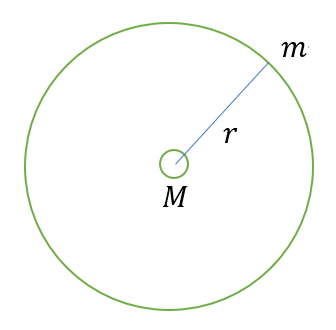
すなわち、一般的に、ある質量をもつ物体から r だけ離れた場所にある物体には、
r の2乗に反比例する加速度が生じるように空間の状態が変化していると考えることができます。
これは、突飛なことではなく、私たちが暮らす地球でも、ありとあらゆるところに、
重力加速度が生じます。しかし、これは、物体を置いた場合に初めて生じていることが
わかるものです。(これは、電磁気学で、電場の概念を獲得するときと同じです)。
この解釈で、同様にして太陽に働く力を考えれば、
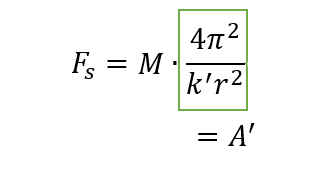
と、表されます。このとき生じる加速度は、物体の質量によって変わってくるはずなので、
別の加速度としています。
ここで、作用反作用の法則によって太陽に働く万有引力と惑星に働く万有引力は等しいので、
万有引力は、M に比例し、m に比例し、rの2乗に反比例することが言えるので、

というように、万有引力の式を導出することができました。
もちろん、これはアナロジー(類推)で、
万有引力は電磁気学で電場を習う時に登場するガウスの法則を使って、
r の2乗に反比例するのだ、というのは感覚的には分かるのですが、
導出過程について、電場を学ぶ際に登場する、場の考え方を取り入れて解釈してみると、
すこしすっきりするかな、と思ったので、記録を兼ねて、書いてみました。
皆様の物理の勉強の参考になれば幸いです。
万有引力の導出の授業をするときに、毎年しっくりきていなかったのですが、
自分なりに少し理解が進んだように思うので、記録しておこうと思います。
具体的には、万有引力の導出で私が毎年もやっとしていたポイントは、
惑星の向心力を求めた後、作用反作用の法則から、太陽についても同じように力が働くので・・・と論を運ぶところにあります。
しかも、太陽は円運動していないのに、円運動から導出した万有引力の式を
そのまま使ってよいのか(しかも、ちゃっかり、惑星の質量を太陽の質量に置き換えている)
これについて、次のように、考えてみました。
さて。
万有引力の導出は、
(ⅰ)惑星の円運動の運動方程式
(ⅱ)ケプラーの第三法則
この2つの式を同時に満たす関係式を作ることから、
惑星に働く向心力(万有引力)を求めるという手順で進めていきます。
(ⅱ)式を変形して、
これを(ⅰ)式に代入して、整理すれば、惑星に働く向心力が
と求まるわけですが、ここで、質量 m 以外の部分は、運動方程式 ma = F であることから、
加速度を表しているはずです。
すなわち、一般的に、ある質量をもつ物体から r だけ離れた場所にある物体には、
r の2乗に反比例する加速度が生じるように空間の状態が変化していると考えることができます。
これは、突飛なことではなく、私たちが暮らす地球でも、ありとあらゆるところに、
重力加速度が生じます。しかし、これは、物体を置いた場合に初めて生じていることが
わかるものです。(これは、電磁気学で、電場の概念を獲得するときと同じです)。
この解釈で、同様にして太陽に働く力を考えれば、
と、表されます。このとき生じる加速度は、物体の質量によって変わってくるはずなので、
別の加速度としています。
ここで、作用反作用の法則によって太陽に働く万有引力と惑星に働く万有引力は等しいので、
万有引力は、M に比例し、m に比例し、rの2乗に反比例することが言えるので、
というように、万有引力の式を導出することができました。
もちろん、これはアナロジー(類推)で、
万有引力は電磁気学で電場を習う時に登場するガウスの法則を使って、
r の2乗に反比例するのだ、というのは感覚的には分かるのですが、
導出過程について、電場を学ぶ際に登場する、場の考え方を取り入れて解釈してみると、
すこしすっきりするかな、と思ったので、記録を兼ねて、書いてみました。
皆様の物理の勉強の参考になれば幸いです。
